Search algorithms

By Afshine Amidi and Shervine Amidi

Basic search

Linear search

Linear search is a basic search method often used when the relative ordering of elements is not known, e.g. in unsorted arrays. It has a complexity of $\mathcal{O}(n)$ time and $\mathcal{O}(1)$ space:

• Scan step: Check whether the constraint of the problem is verified on the first element of the array.

  

  Repeat the process on the remaining elements in a sequential way.

  

• Final step: Stop the search when the desired condition is satisfied.

  

Two-pointer technique

The two-pointer technique provides an efficient way to scan arrays by leveraging the assumptions of the problem, e.g. the fact that an array is sorted.

To illustrate this concept, suppose $A=[a_0, ..., a_{n-1}]$ a sorted array. Given $S$, the goal is to find two elements $a_i, a_j$ such that $a_i+a_j=S$.

The two-pointer technique finds an answer in $\mathcal{O}(n)$ time:

• Initialization: Initialize pointers $l$ and $r$ that are set to be the first and last element of the array respectively.

  

• Compute step: Compute $S_{\textrm{pointers}}\triangleq a_{l}+a_{r}$.

  • Case $S_{\textrm{pointers}} < S$: The computed sum needs to increase, so we move the $l$ pointer to the right.

    

  • Case $S_{\textrm{pointers}} > S$: The computed sum needs to decrease, so we move the $r$ pointer to the left.

    

• Final step: Repeat the compute step until one of the following situations happens:

  • Case $l=r$: There is no solution to the problem.

    

  • Case $S_{\textrm{pointers}}=S$: A solution is found with $i=l$ and $j=r$.

    

Trapping rain water

A classic problem that uses the two-pointer technique is the trapping rain water problem. Given a histogram $H=[h_0, ..., h_{n-1}]$ that represents the height $h_i\geqslant0$ of each building $i$, the goal is to find the total volume $V$ of water that can be trapped between the buildings.

Tricks

• The maximum volume of water $v_i$ trapped at index $i$ is determined by the relative height between $h_i$ and the tallest buildings on the left $h_l^{M}$ and on the right $h_r^{M}$:

  $$\boxed{v_i=\min(h_l^M, h_r^M)-h_i}$$

• Use the two-pointer technique to efficiently update $h_l^M$ and $h_r^M$ at each step.

The solution is found in $\mathcal{O}(n)$ time and $\mathcal{O}(1)$ space:

• Initialization:

  • Pointers: Set the left and right pointers to $l=0$ and $r=n-1$.

  • Maximum heights: Set the maximum height of the left buildings $h_l^M$ and the right buildings $h_r^M$ to $h_l$ and $h_r$.

  • Total amount of water: Set the total amount of water $V$ to 0.

    

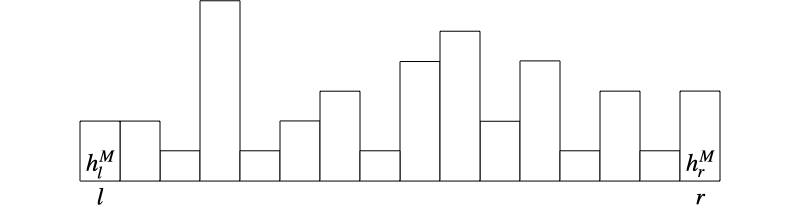
• Compute step: Update the values of the maximum heights of left and right buildings with the current values:

  $$\boxed{h_l^M=\max(h_l^M, h_l)}\quad\textrm{and}\quad\boxed{h_r^M=\max(h_r^M, h_r)}$$

  • If $h_l^M < h_r^M$, then the left side is the limiting side, so:

    • Add the available volume $v_l = h_l^M - h_l$ at index $l$ to the total amount of water $V$:

      $$\boxed{V\longleftarrow V+v_l}$$

    • Move the left pointer to the right:

      $$\boxed{l\longleftarrow l+1}$$

      

  • Conversely, if $h_l^M \geqslant h_r^M$, then:

    • Add the available volume $v_r = h_r^M - h_{r}$ at index $r$ to the total amount of water $V$:

      $$\boxed{V\longleftarrow V+v_r}$$

    • Move the right pointer to the left:

      $$\boxed{r\longleftarrow r-1}$$

      

• Final step: The algorithm finishes when the two pointers meet, in which case the amount of water is given by $V$.

  

Binary search

Algorithm

Binary search aims at finding a given target value $t$ in a sorted array $A=[a_0, ..., a_{n-1}]$.

This algorithm has a complexity of $\mathcal{O}(\log(n))$ time and $\mathcal{O}(1)$ space:

• Initialization: Choose the lower bound $l$ and the upper bound $r$ corresponding to the desired search space. Here, $l=0$ and $r=n-1$.

  

• Compute step: Compute the middle $m$ of the two bounds:

  $$\boxed{m\triangleq l+\left\lfloor\frac{r-l}{2}\right\rfloor}$$

  The above formula is written in a way that avoids integer overflow in case $l$ and $r$ are too large.

  

  We have the following cases:

  • Case $t<a_m$: Shrink the search space to the left side by updating $r$ to $r=m-1$.

    

  • Case $t>a_m$: Shrink the search space to the right side by updating $l$ to $l=m+1$.

    

  • Case $t=a_m$: We found a solution.

    

• Final step: Repeat the compute step until one of the following situations happens:

  • Case $t=a_m$: A solution is found.

  • Case $r<l$: There is no solution since the pointers intersect after fully covering the search space.

Median of sorted arrays

Suppose we want to compute the median of two sorted arrays $A, B$ of respective lengths $n_1, n_2$, with $n_1\leqslant n_2$.

A naive approach would combine the two sorted arrays in $\mathcal{O}(n_1+n_2)$ time, and then select the median of the resulting array. However, a $\mathcal{O}(\log(n_1))$ approach exists that uses binary search in a clever way.

Tricks

• If we categorize all elements of both arrays into:

  • A left partition that has the $\approx\frac{n_1+n_2}{2}$ smallest elements.

  • A right partition that has the $\approx\frac{n_1+n_2}{2}$ biggest elements.

    Then we can deduce the median by looking at the maximum of the left partition and the minimum of the right partition.

• If we know how many elements from $A$ are in the left partition, then we can deduce how many elements from $B$ are in there too.

  

• By noting $A_\textrm{left}, A_\textrm{right}, B_\textrm{left}, B_\textrm{right}$ the left and right partitions from $A$ and $B$, we know the partitioning is done correctly when the following conditions are satisfied:

  $$\textrm{(\textbf{C1}) }\boxed{\max(A_\textrm{left})\leqslant\min(B_\textrm{right})}\quad\textrm{and}\quad\textrm{(\textbf{C2}) }\boxed{\max(B_\textrm{left})\leqslant\min(A_\textrm{right})}$$

  

The binary search solution is based on the position of the partitioning within the array $A$. The solution is found in $\mathcal{O}(\log(n_1))$ time:

• Initialization: We note $i\in[\![0, n_1]\!]$ and $j\in[\![0, n_2]\!]$ the lengths of the left partitions within array $A$ and $B$ respectively. We fix the total size of the left partitions to be $\left\lfloor\frac{n_1+n_2+1}{2}\right\rfloor$.

  

  For a given $i$, the following formula determines $j$:

  $$\boxed{j=\left\lfloor\frac{n_1+n_2+1}{2}\right\rfloor-i}$$

• Binary search: We perform a binary search on $i$ between $0$ and $n_1$.

  

  For each candidate, we have the following cases:

  • (C1) is not satisfied: We restrict the search space to the left side of $i$.

    

  • (C2) is not satisfied: We restrict the search space to the right side of $i$.

    

  • Both (C1) and (C2) are satisfied: The partitioning is done correctly.

    

• Final result: Once the correct partitioning is found, we deduce the value of the median. We note:

  $$\boxed{\textrm{max}_{\textrm{left}}\triangleq\max(A_\textrm{left}, B_\textrm{left})}\quad\textrm{and}\quad\boxed{\textrm{min}_\textrm{right}\triangleq\min(A_\textrm{right}, B_\textrm{right})}$$

We have:

Case	Result	Illustration
$n_1+n_2$ even	$\displaystyle\textrm{median}=\frac{\textrm{max}_\textrm{left}+\textrm{min}_\textrm{right}}{2}$
$n_1+n_2$ odd	$\displaystyle\textrm{median}=\textrm{max}_\textrm{left}$

Substring search

String pattern matching

Given a string $s=s_0...s_{n-1}$ of length $n$ and a pattern $p=p_0...p_{m-1}$ of length $m$, the string matching problem is about finding whether pattern $p$ appears in string $s$.

We note $s_{i:i+m-1}$ the substring of $s$ of length $m$ that starts from $s_i$ and finishes at $s_{i+m-1}$.

Brute-force approach

The brute-force approach consists of checking whether pattern $p$ matches any possible substring of $s$ of size $m$ in $\mathcal{O}(n\times m)$ time and $\mathcal{O}(1)$ space.

Starting from $i=0$, compare the substring that starts from index $i$ with pattern $p$.

We have the following possible situations:

• One of the characters is not matching: The pattern does not match the associated substring.

  

• All characters are matching: The pattern is found in the string.

  

Knuth-Morris-Pratt algorithm

The Knuth-Morris-Pratt (KMP) algorithm is a string pattern matching algorithm that has a complexity of $\mathcal{O}(n+m)$ time and $\mathcal{O}(m)$ space.

Intuition Avoid starting the pattern search from scratch after a failed match.

We do so by checking whether the pattern matched so far has a prefix that is also a suffix:

• Step 1: Build the prefix-suffix array.

  

• Step 2: Find the pattern in the original string using the prefix-suffix array.

  

Prefix-suffix array construction We want to build an array $Q=[q_0, ..., q_{m-1}]$ where each value $q_i$ has two interpretations:

• It is the length of the largest prefix that is also a suffix in the substring $p_0...p_i$.

  

• It is also the index in the pattern that is right after the prefix.

  

This part has a complexity of $\mathcal{O}(m)$ time and $\mathcal{O}(m)$ space:

• Initialization:

  • By convention, we set $q_{-1}$ to $0$.

  • The element $q_0$ is set to 0 since the substring $p_0$ has a single character.

  • The pointers $i$ and $j$ find the largest prefix that is also a suffix to deduce the value of $q_i$. They are initially set to $i=1$ and $j=0$.

    

• Compute step: Determine the length of the largest prefix that is also a suffix for substring $p_0...p_i$:

  • Case $p_i\neq p_j$ and $j=0$: The substring does not have a prefix that is also a suffix, so we set $q_i$ to 0:

    $$\boxed{q_i\longleftarrow 0}$$

    We increment $i$ by 1.

    

  • Case $p_i=p_j$: The last letter $p_i$ of the substring matches with $p_j$. As a result, the length of the prefix is the length of $p_0...p_j$:

    $$\boxed{q_i\longleftarrow j+1}$$

    We increment both $i$ and $j$ by 1 respectively.

    

  • Case $p_i\neq p_j$ and $j>0$: The substring may have a smaller prefix that is also a suffix:

    $$\boxed{j\longleftarrow q_{j-1}}$$

    We repeat this process until we fall in one of the two previous cases.

    

Linear-time string pattern search We want to efficiently search pattern $p$ in string $s$ using the newly-constructed prefix-suffix array $Q$.

This part has a complexity of $\mathcal{O}(n)$ time and $\mathcal{O}(1)$ space:

• Initialization: The pointers $i$ and $j$ check whether there is a match between each character of the string and the pattern respectively. They are initially set to 0.

• Compute step: We check whether characters $s_{i}$ and $p_{j}$ match.

  • Case $s_{i}=p_{j}$: The characters match. We increment $i$ and $j$ by 1.

    

  • Case $s_{i}\neq p_{j}$: The characters do not match. We determine where we should start our search again by using the information contained in the prefix-suffix array.

    • $q_{j-1}=0$: We need to restart the pattern match from the beginning since there is no prefix/suffix to leverage.

    • $q_{j-1}>0$: We can continue our search after the next largest matched prefix of the pattern.

      We set $j$ to $q_{j-1}$.

      

• Final step: The algorithm stops when one of the following situations happens:

  • Case $j=m$: The pattern has been matched.

  • Case $i=n$ and $j<m$: The whole string has been searched without finding a match.

    

Rabin-Karp algorithm

The Rabin-Karp algorithm is a string pattern matching algorithm that uses a hashing trick. It has an expected time complexity of $\mathcal{O}(n+m)$, but depending on the quality of the hash function, the complexity may increase up to $\mathcal{O}(n\times m)$. The space complexity is $\mathcal{O}(1)$.

Intuition Compute the hash value of the pattern along with those of the substrings of the same length. If the hash values are equal, confirm whether the underlying strings indeed match.

The trick is to choose a hash function $h$ that can deduce $h(s_{i+1:i+m})$ from the hash value of the previous substring $h(s_{i:i+m-1})$ in $\mathcal{O}(1)$ time via a known function $f$:

$$\boxed{h(s_{i+1:i+m})=f(h(s_{i:i+m-1}), h(s_i), h(s_{i+m}))}$$

Algorithm

• Initialization: Given a hash function $h$, we compute the hash value $h(p)$ of the pattern $p$.

  

• Compute step: Starting from index $i=0$, we use the hashing trick to compute the hash value of substring $s_{i:i+m-1}$ that starts from $i$ and that has the same length as $p$ in $\mathcal{O}(1)$ time.

  • Case $h(p)\neq h(s_{i:i+m-1})$: $p$ and $s_{i:i+m-1}$ definitely do not match.

    

  • Case $h(p)=h(s_{i:i+m-1})$: There may be a match between $p$ and $s_{i:i+m-1}$, so we compare $p$ and $s_{i:i+m-1}$.

    • Sub-case $p=s_{i:i+m-1}$: The pattern has been matched.

    • Sub-case $p\neq s_{i:i+m-1}$: There is a collision between the hash values of $p$ and $s_{i:i+m-1}$. Since there is no match, we continue the search.

      

Want more content like this?

Subscribe here to be notified of new Super Study Guide releases!