Stacks and queues
By Afshine Amidi and Shervine Amidi
Stacks
Definition
A stack is a data structure that deals with elements in a Last In First Out (LIFO) order.

In order to do that, it uses the push and pop operations:
| Push | Pop |
|---|---|
| Insert an element on the top of the stack. | Remove the element from the top of the stack and return its value. |
 | 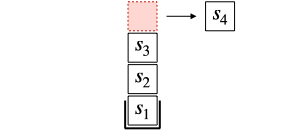 |
As a result, the last element added to the data structure will be the first one removed.
Stacks are commonly used for Depth-First Search (DFS) graph traversals.
Operations
The main operations that can be performed on a stack are explained below:
| Type | Time | Description | Illustration |
|---|---|---|---|
| Access | O(1) | Top of the stack Read the top element. | |
| O(n) | Any other position Depending on the desired position, the stack needs to be popped at most n times. | ||
| Search | O(n) | Depending on whether the desired value gets found right away, the stack needs to be popped at most n times. | |
| Insertion | O(1) | Top of the stack Push the new element. | |
| O(n) | Any other position 1. Pop elements until accessing the desired position and push them into an auxiliary stack. 2. Push the new element. 3. Pop elements from the auxiliary stack and push them into the initial stack. | ||
| Deletion | O(1) | Top of the stack Pop the existing element. | |
| O(n) | Any other position 1. Pop elements until accessing the desired position and push them into an auxiliary stack. 2. Pop the existing element. 3. Pop elements from the auxiliary stack and push them into the initial stack. |
Daily temperatures
Suppose we are given an array of temperatures. For each day , the goal is to find the number of days until there is a warmer temperature.

In other words, for each day , we want to find the number of days such that:
A naive approach would compute the answer for each day in isolation. By scanning up to elements for each day , this approach leads to an overall time complexity of .
However, a more efficient approach uses stacks and computes the solution in time and space:
Initialization:
Initialize an empty stack .
Initialize the output array with zeros.
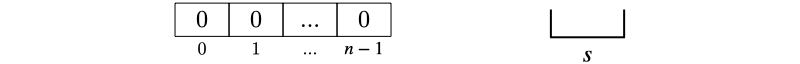
Compute step: We use the monotonic stack trick:
The stack tracks days and their associated temperatures .
Elements added to the stack are days for which we want to find a greater temperature. They are popped as soon as a future warmer day is found.
Temperature values are popped in a monotonically non-decreasing manner. This ensures that all relevant values are popped for a given warmer day.
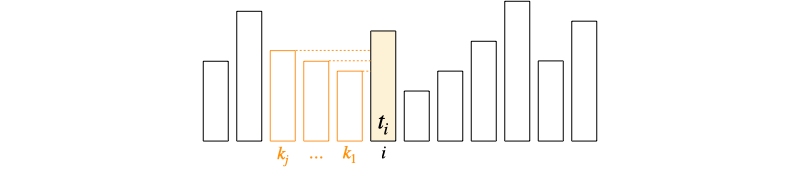
We start from day 0. For each day , we have the following cases:
If the temperature at the top of the stack is lower than the current temperature , pop from the stack, and write the corresponding day difference in the final array:
Repeat the popping procedure until the condition is not satisfied anymore.

Add the current item to the stack .

Repeat this process until reaching the end of the array . The array contains the final answer. Entries with zeros correspond to days that do not have future warmer days.
Queues
Definition
A queue is a data structure that deals with elements in a First In First Out (FIFO) order, where its tail has the most recently arrived elements and its head has elements that arrived the earliest.

In order to do that, it uses the enqueue and dequeue operations:
| Enqueue | Dequeue |
|---|---|
| Insert element at the tail of the queue. | Remove element from the head of the queue. |
 |  |
As a result, the first element added to the data structure will be the first one to be removed.
Queues are commonly used for Breadth-First Search (BFS) graph traversals.
Operations
The main operations that can be performed on a queue are explained below:
| Type | Time | Description | Illustration |
|---|---|---|---|
| Access | O(1) | Head of the queue Read the front element. |  |
| O(n) | Any other position Depending on the desired position, the queue needs be dequeued at most n times. | ||
| Search | O(n) | Depending on whether the desired value gets found right away, the queue needs to be dequeued at most n times. |  |
| Insertion | O(1) | Tail of the queue Enqueue the new element. |  |
| O(n) | Any other position 1. Initialize a new empty queue. 2. Dequeue elements from the current queue and enqueue them to the new queue up until right before the desired position of insertion. 3. Enqueue the new element in the new queue. 4. Dequeue the remaining elements from the current queue and enqueue them to the new queue. | ||
| Deletion | O(1) | Head of the queue Dequeue the existing element. |  |
| O(n) | Any other position 1. Initialize a new empty queue. 2. Dequeue elements from the current queue and enqueue them to the new queue up until right before the desired position of deletion. 3. Dequeue the element to be removed from the current queue and ignore it. 4. Dequeue the remaining elements from the current queue and enqueue them to the new queue. |
Subscribe here to be notified of new Super Study Guide releases!